" 주어진 범위 안에서 특정 숫자 찾기 "
방법1) 숫자를 일일이 다 비교하면서 찾기(순차탐색)
방법2) 이진탐색으로 찾기
[이진탐색]
이진탐색은 Up&Down 게임과 같음!
Up&Down 게임 : 특정 숫자를 맞추는 게임. 정답인 숫자가 더 높다면 "UP", 낮다면 "Down" 을 부르는 게임
위의 게임을 할 때 숫자의 범위를 최대한 줄이는 게 가장 효율적임
만약 1~100 사이의 숫자를 찾아야 한다면, 50을 먼저 외쳐 범위를 1~49 또는 51~100으로 줄이고 게임을 하는게 좋음
이처럼 범위를 절반씩 줄여가면서 찾는게 가장 빨리 찾을 수 있음
이 방법이 바로 "이진탐색"
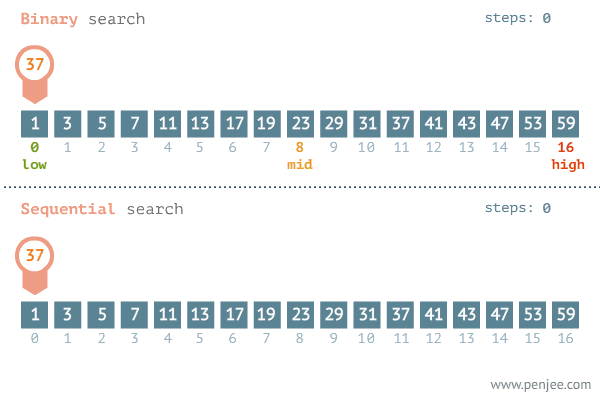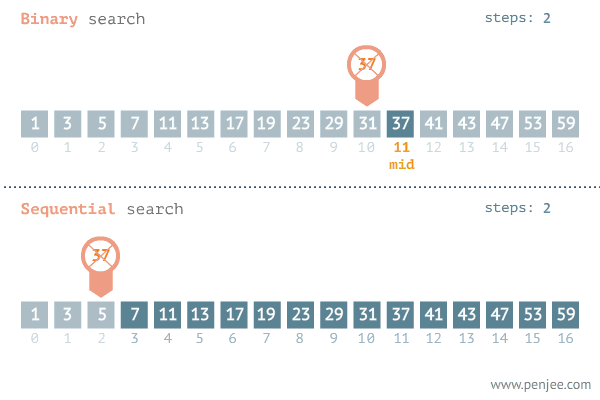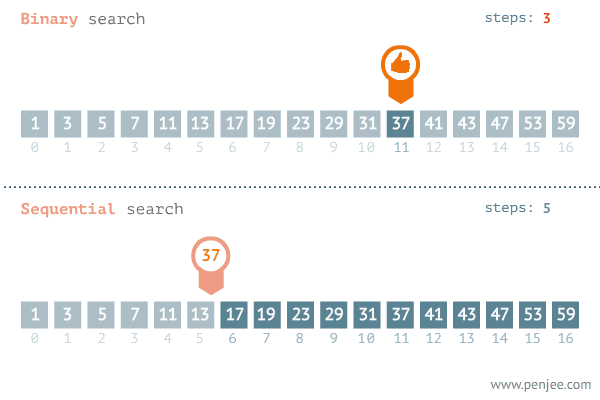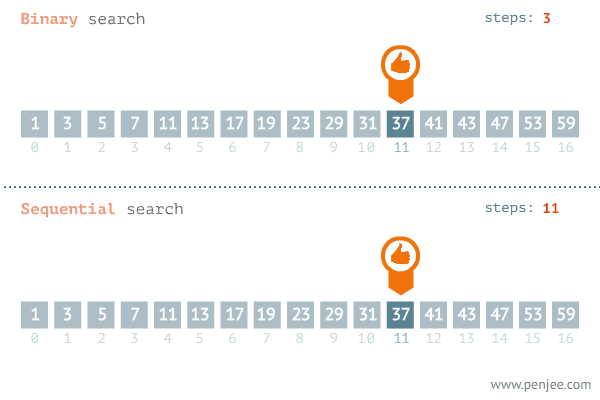
" 그럼, 방법 1이랑 방법 2 둘 중 뭐가 더 효율적일까??! "
[1~16까지 오름차순으로 정렬되어있는 배열 중에서 14 찾기]
방법1) 숫자를 일일이 다 비교하면서 찾기(순차탐색)
finding_target = 14
finding_numbers = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]
def is_existing_target_number_sequential(target, array):
find_count = 0
for number in array:
find_count += 1
if target == number:
print("시도한 횟수:", find_count) # 14!
return True
return False
result = is_existing_target_number_sequential(finding_target, finding_numbers)
print(result) # True
# 시도한 횟수: 14
# True[시간복잡도]
배열을 차례로 따라가면서 찾다보니, 검색횟수가 총 14번이 걸림
만약 찾는 숫자가 16이었다면 16번 검색해야 했을테니 최악의 경우는 O(N) 걸린다고 할 수 있음
방법2) 이진탐색으로 찾기
array 를 따라가면서 target 이 존재한다면 True 를 반환하고, 끝까지 없다면 False 를 반환

시도했을 때 target 보다 작다면 더 큰 값들을 뒤져야 하니까 최솟값에 시돗값 + 1 을 대입
시도했을 때 target 보다 크다면 더 작은 값들을 뒤져야 하니까 최댓값에 시돗값 - 1 을 대입
이를 최솟값 ≤ 최댓값 까지 반복!
왜 < 가 아니라 ≤ 냐면 최솟값 == 최댓값인 시점까지 확인을 해야 하기 때문!
finding_target = 14
finding_numbers = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]
def is_existing_target_number_binary(target, array):
current_min = 0
current_max = len(array) - 1
count = 0
while current_min <= current_max:
current_guess = (current_min + current_max) // 2
count += 1
if array[current_guess] == target:
print("시도한 횟수: ", count)
return True
elif array[current_guess] < target:
current_min = current_guess + 1
else:
current_max = current_guess - 1
print("시도한 횟수: ", count)
return False
result = is_existing_target_number_binary(finding_target, finding_numbers)
print(result)
# 시도한 횟수: 3
# True[시간복잡도]
총 숫자가 1~N 까지이면
1번 탐색) 절반이 줄어듦: N/2 개 남음
2번 탐색) 절반이 줄어듦: N/4 = N/(2^2) 개 남음
3번 탐색) 절반이 줄어듦: N/8 = N/(2^3) 개 남음
....
k번 탐색) 절반이 줄어듦: N/(2^k) 개 남음
이 때, 이분탐색을 열심히 시도해서 딱 1개만 남았다고 가정!
이걸 수식으로 표현하면, N/(2^k) = 1
-> k = log_2{N} 횟수를 시도하면 정답을 찾을 수 있음
결론) 시간 복잡도가 O(logN) 만큼 걸린다. 라고 말할 수 있음
왜 log_2N 이 아니라 logN 인가요?
상수는 무시해도 되기 때문에 표기하기 쉽도록 logN 으로 부르기로 약속했음
연산량이 반으로 나눠진다 싶으면 O(logN) 이겠구나 하면 됨
[내가 만든 코드]
finding_target = 14
finding_numbers = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]
def is_existing_target_number_binary(target, array):
min_num = array[0]
max_num = array[-1]
try_num = 0
count = 0
if target > len(array):
return "None!!"
while target != try_num:
try_num = (min_num + max_num) // 2
count += 1
if try_num < target:
min_num = try_num + 1
elif try_num > target:
max_num = try_num - 1
print("시도한 횟수: ", count)
return try_num
result = is_existing_target_number_binary(finding_target, finding_numbers)
print(result)
# 시도한 횟수: 3
# 14정리
'알고리즘' 카테고리의 다른 글
| 재귀함수 - 2 (0) | 2021.08.24 |
|---|---|
| 재귀함수 - 1 (0) | 2021.08.23 |
| 링크드 리스트 문제 (0) | 2021.08.22 |
| 링크드 리스트 구현 - 2 (0) | 2021.08.22 |
| 링크드 리스트 구현 - 1 (0) | 2021.08.21 |